Однопозиционный пространственно-временной континуум.

1. Существует квант пространства

2. Существует квант времени.

При этом мы не утверждаем, что они существуют в качестве ЯВЛЕНИЙ в реальном мире. Нам они нужны как постулаты для геометрии.

Так же мы помним про первые главы о пространственноцентричном мышлении. Кроме того у нас для мышления есть: Объект, субъект, абстракция. И есть уровни нашего восприятия: явления, феномены, идеи.

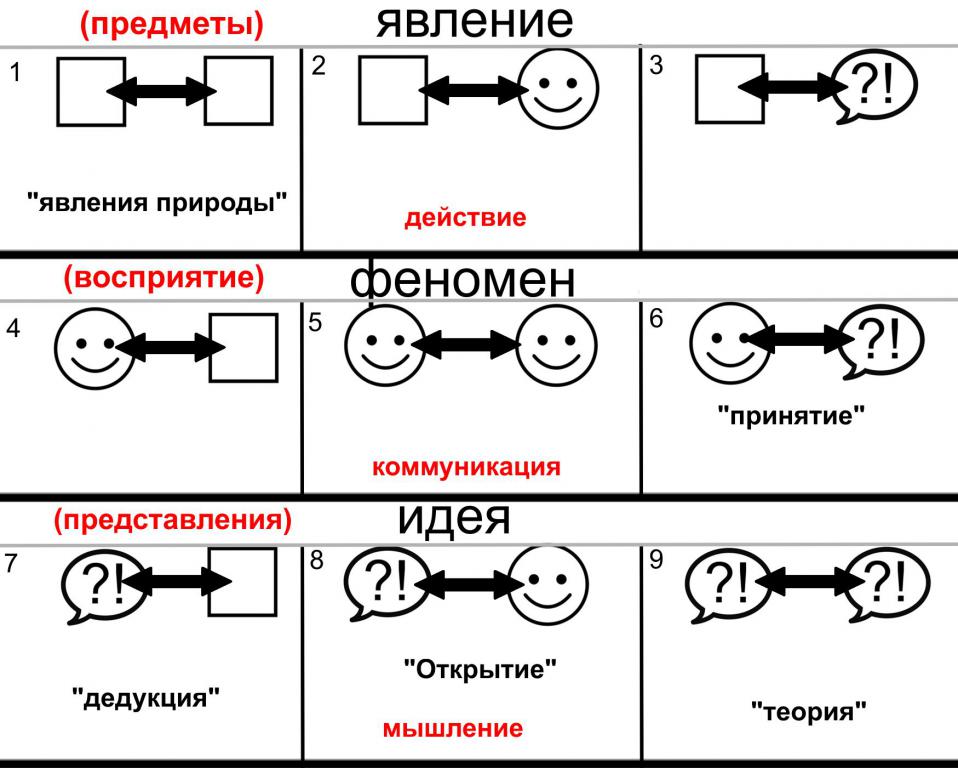
Если мы представим, что у нас в один момент времени (кванте времени) в одном месте (кванте пространства) существует только один объект (или на ваше усмотрение субъект и абстракция) то мы получаем простой однопозиционный пространственно-временной континуум (ПВК). Или проще - однопозиционное время, имея ввиду, что это конечно не только время, но и пространство, которые определенным образом взаимодействуют. Это время в явлениях отлично прописано классической механикой и формальной логикой.

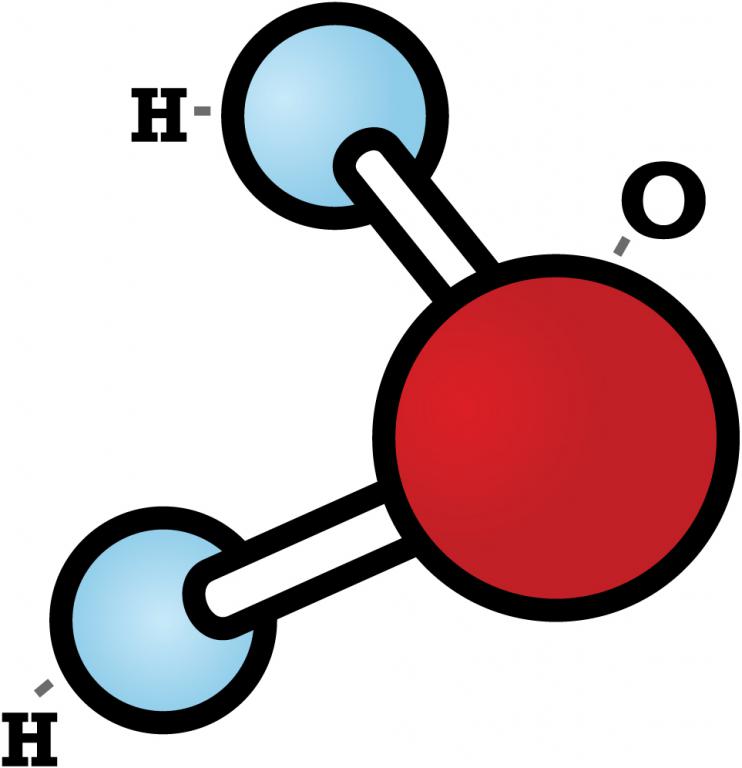
На рисунке вы видите схематичное изображение молекулы воды. В нем два атома водорода. Так вот, атом водорода не может быть одновременно частью молекулы воды и, допустим, перекиси водорода.

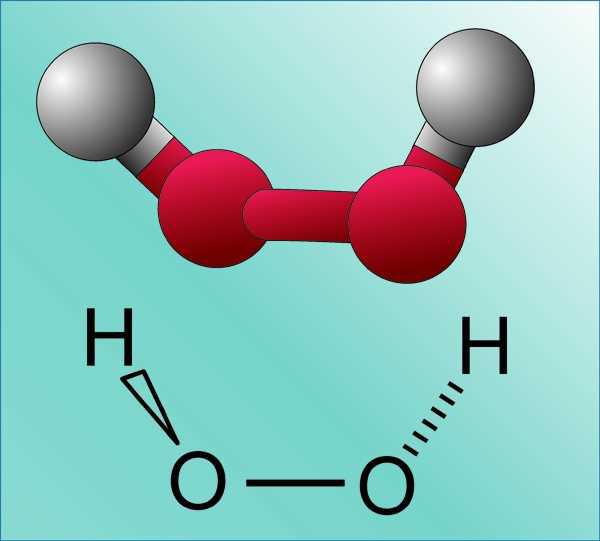
На рисунке схематичное изображение молекулы перекиси водорода.

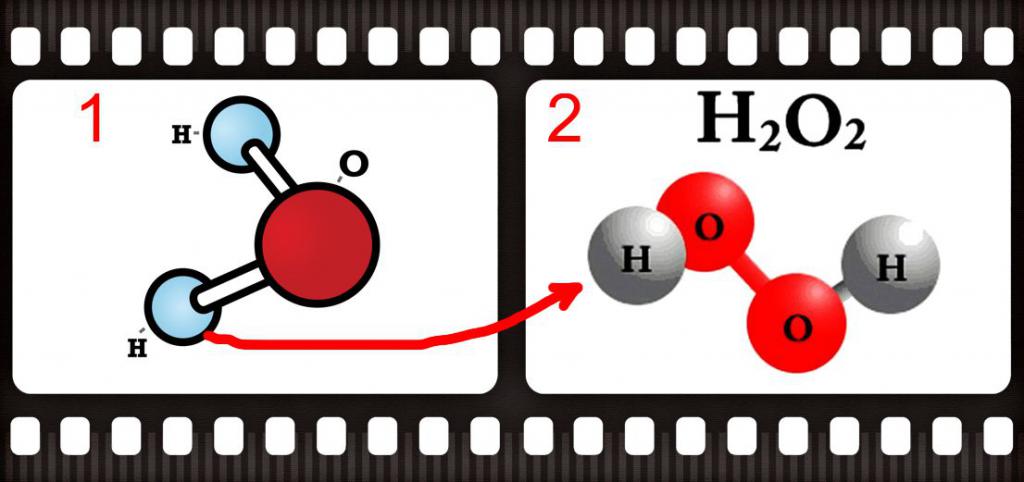
На картинке мы видим как бы сменяющие друг друга кадры кинопленки. В одном наш герой (атом) состоит в одной молекуле. А во втором кадре уже перескакивает в другую молекулу. Но одновременно в ОДНОМ КАДРЕ в обеих молекулах он быть не может.

Интересный факт, что когда автор рассказывал эту простую вещь на лекциях, то она НЕ БЫЛА очевидна для всех присутствующих! )))

Разумеется популярная игра Майнкрафт об этом же. В ней мир собран из явных кирпичиков.

Но довольно часто в жизни людей происходит именно однопозиционное восприятие. Когда происходит нечто, и яркие ощущения фиксируют в нашей памяти идею или просто событие. Происходит то, что мы назвали в прошлых частях «принятием».

На картинке изображен древнегреческий мыслитель Архимед в момент открытия закона о вытесненном объеме жидкости.

Увы, чаще происходит, другая картина, когда мы, увидели лишь часть реальности, получили «принятие», и восторженно считаем, что это… квадрат. А кто-то наблюдал с другой стороны и увидел круг. И начинается столкновение личных однопозиционных времен.

А на самом деле это был цилиндр…

Если вы поняли главную суть однопозиционного времени, что в одном кванте пространства в один квант времени может быть только один объект или что в одном месте в одно время одна вещь, то законы формальной логики вам сразу становятся просты и понятны ( и не нужны )))

Формальная логика объясняет явления в физическом мире и сама по себе является отражением в слое идей однопозиционного пространственно-временного континуума.

Кстати, очевидным выводом из определения однопозиционного времени является так называемый «закон сохранения энергии».

Если мы принимаем постулат, что в одном месте в один момент времени может быть только один объект (квант), то дальше остается только вычислить опытным и теоретическим путем, каким образом объекты переходят от одного скопления (картинки в нашем восприятии) к другому скоплению. И получаем механистическую картину мира Ньютона. Эта картина царила вплоть до 20-го века, когда наука наткнулась на более сложные времена, но до сих пор пытается там работать все в той же однопозиционной логике.

А ведь еще другой древнегреческий мыслитель Платон в некоторых своих произведениях показал, что такая логика ограниченна. Уже в социальном пространстве она не работает. Но мы будем рассматривать это в следующей части.

Хотя это вовсе не значит, что в однопозиционной реальности, наука не права )))

Шашки – игра, которая, как и шахматы, ярко иллюстрирует однопозиционное время. А в следующей части будет приведена игра, которая иллюстрирует суперпозиционное время.